-------------------------------------------------------------------------------
Example presentation: stdtable, a package to standardize tables --
standardizing cross-tabulations
-------------------------------------------------------------------------------
The influence of marginal distributions
Consider the example below
It shows the race of the husband and the race of the wife for couples
living in the USA that got married between 2010 and 2017
The races are very unequaly distributed in the USA
We can control for one marginal distribution by computing row or collumn
percentages.
. use homogamy, clear
(American Community Survey 2008-2017)
. tab racem racef [fw=freq] if marcoh == 2010, row nofreq
race, | race, wife
husband | white hispanic black native asian | Total
-----------+-------------------------------------------------------+----------
white | 89.55 5.16 0.76 0.38 2.56 | 100.00
hispanic | 18.25 77.54 1.19 0.27 1.55 | 100.00
black | 13.02 5.46 77.49 0.24 1.40 | 100.00
native | 46.04 6.90 1.44 41.55 2.19 | 100.00
asian | 9.83 2.60 0.42 0.07 85.64 | 100.00
other | 46.29 11.58 5.20 0.68 7.83 | 100.00
-----------+-------------------------------------------------------+----------
Total | 64.27 17.56 8.14 0.55 7.36 | 100.00
race, | race, wife
husband | other | Total
-----------+-----------+----------
white | 1.60 | 100.00
hispanic | 1.20 | 100.00
black | 2.39 | 100.00
native | 1.89 | 100.00
asian | 1.43 | 100.00
other | 28.42 | 100.00
-----------+-----------+----------
Total | 2.12 | 100.00
We see racial homogamy: people tend to marry someone of the same race
However, several things are hard to see in this table:
Are whites really the most closed group or is there a substantial
"colorblind" group of whites that accidentally married another white
because that is the largest group?
Are Native Americans really so much less homogamous or are we seeing
an artifact caused by the small number of native american women
(0.6%)?
If native Americans were mixing around randomly, then we would expect
much less native american males marrying native american females.
Apperently native American men still prefer native American women but
because there are so many other women around he will still have a
good chance of eventually marrying another women.
Is there symetery in this table, e.g. are hispanic males as likely to
marry a white female as hispanic females are to marry white males?
It does not seem to be the case from this table, but 5% from all
white males could be similar to 18% from all hispanic males.
There is something mechanical about the influence of the margins, and it
is common (in sociology) to want to look at the pattern in the table nett
of this influence of the marginal distributions.
We could do this by looking at >> odds ratios, but here I want to show an
alternative.
-------------------------------------------------------------------------------
index >>
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
Example presentation: stdtable, a package to standardize tables --
standardizing cross-tabulations
-------------------------------------------------------------------------------
Standardizing tables
When we do a chi squared test for cross-tabulations we compare observed
cell counts with predicted cell counts
For these predicted cell counts we assume that the margins remain as
observed, but otherwise there is no association between the variables
(the odds ratios are all 1).
In the table of predicted cell counts the only pattern is due to the
margins.
. tab racem racef [fw=freq] if marcoh==2010, exp
+--------------------+
| Key |
|--------------------|
| frequency |
| expected frequency |
+--------------------+
race, | race, wife
husband | white hispanic black native asian | Total
-----------+-------------------------------------------------------+----------
white |31,956,989 1,842,451 270,679 134,486 911,938 |35,687,890
|22935235.6 6267911.2 2904780.0 197,859.6 2625311.4 |35687890.0
-----------+-------------------------------------------------------+----------
hispanic | 1,716,537 7,292,537 111,903 25,163 145,556 | 9,404,856
| 6044139.6 1651787.3 765,498.8 52,142.1 691,850.2 | 9404856.0
-----------+-------------------------------------------------------+----------
black | 674,410 282,817 4,014,816 12,534 72,745 | 5,181,272
| 3329804.4 909,993.6 421,724.4 28,725.8 381,150.4 | 5181272.0
-----------+-------------------------------------------------------+----------
native | 136,200 20,397 4,253 122,904 6,469 | 295,799
| 190,098.7 51,951.6 24,076.3 1,640.0 21,759.9 | 295,799.0
-----------+-------------------------------------------------------+----------
asian | 323,750 85,783 13,922 2,216 2,820,542 | 3,293,314
| 2116486.4 578,409.1 268,056.0 18,258.7 242,266.3 | 3293314.0
-----------+-------------------------------------------------------+----------
other | 494,673 123,760 55,546 7,248 83,703 | 1,068,672
| 686,794.4 187,692.3 86,983.5 5,924.9 78,614.8 | 1068672.0
-----------+-------------------------------------------------------+----------
Total |35,302,559 9,647,745 4,471,119 304,551 4,040,953 |54,931,803
|35302559.0 9647745.0 4471119.0 304,551.0 4040953.0 |54931803.0
race, | race, wife
husband | other | Total
-----------+-----------+----------
white | 571,347 |35,687,890
| 756,792.3 |35687890.0
-----------+-----------+----------
hispanic | 113,160 | 9,404,856
| 199,438.0 | 9404856.0
-----------+-----------+----------
black | 123,950 | 5,181,272
| 109,873.3 | 5181272.0
-----------+-----------+----------
native | 5,576 | 295,799
| 6,272.7 | 295,799.0
-----------+-----------+----------
asian | 47,101 | 3,293,314
| 69,837.5 | 3293314.0
-----------+-----------+----------
other | 303,742 | 1,068,672
| 22,662.1 | 1068672.0
-----------+-----------+----------
Total | 1,164,876 |54,931,803
| 1164876.0 |54931803.0
Can't we reverse that? Keep the association (odds ratios) as observed but
fix the margins.
For example we could fix all margins at a 100.
That way we can look at the proportion native American men marrying
native American women when they weren't such a small group.
This is what standardizing tables does (Yule 1912). This is implemented
in the stdtable package.
. stdtable racem racef [fw=freq] if marcoh == 2010
-------------------------------------------------------------------------------
race, | race, wife
husband | white hispanic black native asian other Total
---------+---------------------------------------------------------------------
white | 67.3 8.29 2.72 4.88 4.87 11.9 100
hispanic | 8.69 78.9 2.71 2.19 1.87 5.68 100
black | 3.05 2.74 86.8 .978 .835 5.56 100
native | 5.7 1.82 .851 88.6 .686 2.31 100
asian | 3.94 2.23 .809 .464 86.9 5.67 100
other | 11.3 6.05 6.07 2.86 4.85 68.9 100
|
Total | 100 100 100 100 100 100 600
-------------------------------------------------------------------------------
stdtable is thus very useful in conjunction with a chi-squared test for
cross-tabulations:
The chi-squared test tells you whether or not there is a pattern in
the table on top of what is imposed by the margins.
stdtable tells you what that pattern is.
-------------------------------------------------------------------------------
<< index >>
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
Example presentation: stdtable, a package to standardize tables --
standardizing cross-tabulations
-------------------------------------------------------------------------------
Displaying results from stdtable
We can add options to make the table look better
. stdtable racem racef [fw=freq] if marcoh == 2010, ///
> format(%5.0f)
-------------------------------------------------------------------------------
race, | race, wife
husband | white hispanic black native asian other Total
---------+---------------------------------------------------------------------
white | 67 8 3 5 5 12 100
hispanic | 9 79 3 2 2 6 100
black | 3 3 87 1 1 6 100
native | 6 2 1 89 1 2 100
asian | 4 2 1 0 87 6 100
other | 11 6 6 3 5 69 100
|
Total | 100 100 100 100 100 100 600
-------------------------------------------------------------------------------
We can compare across groups
. stdtable racem racef [fw=freq], by(marcoh) format(%5.0f)
--------------------------------------------------------------------------
mariage |
cohort |
and race, | race, wife
husband | white hispanic black native asian other Total
----------+---------------------------------------------------------------
1950-1959 |
white | 88 2 0 3 1 5 100
hispanic | 3 95 0 1 0 1 100
black | 0 0 97 0 0 2 100
native | 3 1 1 93 0 3 100
asian | 1 1 0 0 95 3 100
other | 6 1 2 2 3 86 100
|
Total | 100 100 100 100 100 100 600
----------+---------------------------------------------------------------
1960-1969 |
white | 86 3 0 4 2 6 100
hispanic | 3 94 0 1 0 1 100
black | 0 0 96 0 0 2 100
native | 4 1 0 93 0 2 100
asian | 1 1 0 0 95 3 100
other | 6 1 2 2 2 86 100
|
Total | 100 100 100 100 100 100 600
----------+---------------------------------------------------------------
1970-1979 |
white | 82 4 0 5 2 6 100
hispanic | 4 92 1 1 1 2 100
black | 1 1 95 1 1 2 100
native | 5 1 1 91 0 2 100
asian | 2 1 0 0 94 3 100
other | 6 2 3 2 2 84 100
|
Total | 100 100 100 100 100 100 600
----------+---------------------------------------------------------------
1980-1989 |
white | 79 5 1 5 3 7 100
hispanic | 5 89 1 2 1 2 100
black | 1 1 94 1 1 3 100
native | 5 1 1 91 1 2 100
asian | 2 1 0 0 93 4 100
other | 8 3 3 2 3 82 100
|
Total | 100 100 100 100 100 100 600
----------+---------------------------------------------------------------
1990-1999 |
white | 75 6 2 5 3 9 100
hispanic | 6 87 2 2 1 3 100
black | 2 1 92 1 1 3 100
native | 6 1 1 89 0 3 100
asian | 2 1 0 1 91 4 100
other | 9 3 3 3 3 79 100
|
Total | 100 100 100 100 100 100 600
----------+---------------------------------------------------------------
2000-2009 |
white | 70 8 2 5 4 10 100
hispanic | 7 82 2 3 1 5 100
black | 2 2 89 1 1 4 100
native | 6 2 1 88 1 3 100
asian | 3 2 1 1 88 5 100
other | 10 5 5 2 5 73 100
|
Total | 100 100 100 100 100 100 600
----------+---------------------------------------------------------------
2010-2017 |
white | 67 8 3 5 5 12 100
hispanic | 9 79 3 2 2 6 100
black | 3 3 87 1 1 6 100
native | 6 2 1 89 1 2 100
asian | 4 2 1 0 87 6 100
other | 11 6 6 3 5 69 100
|
Total | 100 100 100 100 100 100 600
--------------------------------------------------------------------------
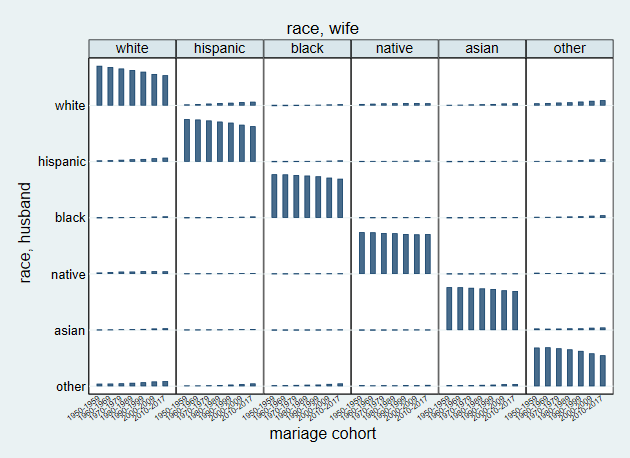
Alternatively we can replace the data in memory with standardized counts
and use those to create a graph
. qui stdtable racem racef [fw=freq], ///
> by(marcoh) replace
.
. tabplot racem marcoh [iw=std], ///
> by(racef, compact note("") cols(6) ///
> t1title("race, wife")) ///
> xlab( 1(1)7, angle(35) labsize(vsmall) )
-------------------------------------------------------------------------------
<< index >>
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
Example presentation: stdtable, a package to standardize tables -- Estimation
-------------------------------------------------------------------------------
Iterative Proportional fitting
The idea to change the margins to be all 100, but otherwise leave
everything as much as possible the same.
We know how to do that for just row totals:
divide all cells by its rowtotal and multiply by 100
. use homogamy, clear
(American Community Survey 2008-2017)
. tab racem racef [fw=freq] if marcoh == 2010, matcell(data)
race, | race, wife
husband | white hispanic black native asian | Total
-----------+-------------------------------------------------------+----------
white |31,956,989 1,842,451 270,679 134,486 911,938 |35,687,890
hispanic | 1,716,537 7,292,537 111,903 25,163 145,556 | 9,404,856
black | 674,410 282,817 4,014,816 12,534 72,745 | 5,181,272
native | 136,200 20,397 4,253 122,904 6,469 | 295,799
asian | 323,750 85,783 13,922 2,216 2,820,542 | 3,293,314
other | 494,673 123,760 55,546 7,248 83,703 | 1,068,672
-----------+-------------------------------------------------------+----------
Total |35,302,559 9,647,745 4,471,119 304,551 4,040,953 |54,931,803
race, | race, wife
husband | other | Total
-----------+-----------+----------
white | 571,347 |35,687,890
hispanic | 113,160 | 9,404,856
black | 123,950 | 5,181,272
native | 5,576 | 295,799
asian | 47,101 | 3,293,314
other | 303,742 | 1,068,672
-----------+-----------+----------
Total | 1,164,876 |54,931,803
.
. mata
------------------------------------------------- mata (type end to exit) -----
: data = st_matrix("data")
:
: muhat = data
:
: muhat = muhat:/rowsum(muhat):*100
: end
-------------------------------------------------------------------------------
We could do the same with the column totals
. mata
------------------------------------------------- mata (type end to exit) -----
: muhat = muhat:/colsum(muhat):*100
: colsum(muhat)
1 2 3 4 5 6
+-------------------------------------+
1 | 100 100 100 100 100 100 |
+-------------------------------------+
: rowsum(muhat)
1
+---------------+
1 | 53.49494192 |
2 | 85.94806215 |
3 | 108.846317 |
4 | 132.1110102 |
5 | 95.96333662 |
6 | 123.6363322 |
+---------------+
: end
-------------------------------------------------------------------------------
This is close, but not quite.
What happens when we repeat that a couple of times
. mata
------------------------------------------------- mata (type end to exit) -----
: muhat = muhat:/rowsum(muhat):*100
: muhat = muhat:/colsum(muhat):*100
:
: muhat = muhat:/rowsum(muhat):*100
: muhat = muhat:/colsum(muhat):*100
:
: muhat = muhat:/rowsum(muhat):*100
: muhat = muhat:/colsum(muhat):*100
:
: muhat = muhat:/rowsum(muhat):*100
: muhat = muhat:/colsum(muhat):*100
: colsum(muhat)
1 2 3 4 5 6
+-------------------------------------+
1 | 100 100 100 100 100 100 |
+-------------------------------------+
: rowsum(muhat)
1
+---------------+
1 | 98.64518228 |
2 | 97.08558589 |
3 | 101.6611192 |
4 | 106.2503037 |
5 | 97.30651588 |
6 | 99.05129309 |
+---------------+
: end
-------------------------------------------------------------------------------
Again, better and we can imagine that with some extra iterations we would
get where we want to be.
This is iterative proportional fitting (Kruithof 1937; Deming and Stephan
1940)
-------------------------------------------------------------------------------
<< index >>
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
How to create a smcl presentation -- creating the presentation
-------------------------------------------------------------------------------
Getting started
I start with creating a folder for my presentation, with three
sub-folders:
source
presentation
handout
I then start brainstorming about what I want to do in my presentation.
I typically do this in a text file in the source directory, that will
later become a .do file, so I put the text in comments
Here is the .do file for the example presentation
// -------- A section standardizing cross-tabulations
// illustrate the impact of the marginal distribution in cross-tabulations with
// an example
// a digression on odds ratios
// Show how the chi-squared test deals with marginal distributions
// Standardizing tables as the reverse of chi-squared test
// -------- A section on Iterative proportional fitting
// use Mata to repeatedly make all row totals a 100, and all column totals 100
// a appendix showing that not all tables can be standardized
Next step is to create the examples
// -------- A section standardizing cross-tabulations
// illustrate the impact of the marginal distribution in cross-tabulations with
// an example
use homogamy, clear
tab racem racef [fw=freq] if marcoh == 2010, row nofreq
// a digression on odds ratios
tab racem racef [fw=freq] if marcoh == 2010
di 122904 / 136200
di 134486 / 31956989
di (122904 / 136200)/(134486 / 31956989)
// Show how the chi-squared test deals with marginal distributions
tab racem racef [fw=freq] if marcoh==2010, exp
// Standardizing tables as the reverse of chi-squared test
stdtable racem racef [fw=freq] if marcoh == 2010
// show how to make the table look better, compare groups, and turn it into a graph
stdtable racem racef [fw=freq] if marcoh == 2010, ///
format(%5.0f)
stdtable racem racef [fw=freq], by(marcoh) format(%5.0f)
qui stdtable racem racef [fw=freq], ///
by(marcoh) replace
tabplot racem marcoh [iw=std], ///
by(racef, compact note("") cols(6) ///
t1title("race, wife")) ///
xlab( 1(1)7, angle(35) labsize(vsmall) )
// -------- A section on Iterative proportional fitting
// use Mata to repeatedly make all row totals a 100, and all column totals 100
use homogamy, clear
tab racem racef [fw=freq] if marcoh == 2010, matcell(data)
mata
data = st_matrix("data")
muhat = data
muhat = muhat:/rowsum(muhat):*100
end
mata
muhat = muhat:/colsum(muhat):*100
colsum(muhat)
rowsum(muhat)
end
mata
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
colsum(muhat)
rowsum(muhat)
end
// a appendix showing that not all tables can be standardized
/*
0 0 2
1 5 2
8 7 0
*/
Next step is to Indicate when a slide begins with //slide and ends with
//endslide
With the //title one specifies the title of the slide
Examples are indicated by //ex and //endex
Indicate any datasets or other files that the presentation needs with
//file filename
Sections are indicated by //section section_name
This is what we get:
//section standardizing cross-tabulations
//slide ------------------------------------------------------------------------
//title The influence of marginal distributions
//ex
use homogamy, clear
tab racem racef [fw=freq] if marcoh == 2010, row nofreq
//endex
//endslide ---------------------------------------------------------------------
//slide ------------------------------------------------------------------------
//title Odds ratios
//ex
tab racem racef [fw=freq] if marcoh == 2010
di 122904 / 136200
di 134486 / 31956989
di (122904 / 136200)/(134486 / 31956989)
//endex
//endslide ---------------------------------------------------------------------
//slide ------------------------------------------------------------------------
//title Standardizing tables
//ex
tab racem racef [fw=freq] if marcoh==2010, exp
//endex
//ex
stdtable racem racef [fw=freq] if marcoh == 2010
//endex
//endslide ---------------------------------------------------------------------
//slide ------------------------------------------------------------------------
//title Displaying results from stdtable
//ex
stdtable racem racef [fw=freq] if marcoh == 2010, ///
format(%5.0f)
//endex
//ex
stdtable racem racef [fw=freq], by(marcoh) format(%5.0f)
//endex
//ex
qui stdtable racem racef [fw=freq], ///
by(marcoh) replace
tabplot racem marcoh [iw=std], ///
by(racef, compact note("") cols(6) ///
t1title("race, wife")) ///
xlab( 1(1)7, angle(35) labsize(vsmall) )
//endex
//endslide ---------------------------------------------------------------------
//section Estimation
//slide ------------------------------------------------------------------------
//title Iterative Proportional fitting
//ex
use homogamy, clear
tab racem racef [fw=freq] if marcoh == 2010, matcell(data)
mata
data = st_matrix("data")
muhat = data
muhat = muhat:/rowsum(muhat):*100
end
//endex
//ex
mata
muhat = muhat:/colsum(muhat):*100
colsum(muhat)
rowsum(muhat)
end
//endex
//ex
mata
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
colsum(muhat)
rowsum(muhat)
end
//endex
//endslide ---------------------------------------------------------------------
//slide ------------------------------------------------------------------------
//title Can all tables be standardized?
/*
0 0 2
1 5 2
8 7 0
*/
//endslide ---------------------------------------------------------------------
This is already a sourcefile we can use for smclpres
. smclpres using stdtable\source\stdtable03.do , replace dir(stdtable/presentat
> ion)
to view the presentation:
first change the directory to where the presentation is stored:
cd "D:\Mijn
documenten\projecten\stata\sug\london19\buis_smclpres\presentation\stdtable\pre
> sentation"
Then type:
view stdtable03.smcl
. cd stdtable/presentation
D:\Mijn documenten\projecten\stata\sug\london19\buis_smclpres\presentation\stdt
> able\presentation
. dir
<dir> 9/03/19 10:06 .
<dir> 9/03/19 10:06 ..
6.3k 8/06/19 11:07 homogamy.dta
0.5k 9/03/19 10:06 slide1.smcl
0.1k 9/03/19 10:06 slide1ex1.do
0.5k 9/03/19 10:06 slide2.smcl
0.1k 9/03/19 10:06 slide2ex1.do
0.6k 9/03/19 10:06 slide3.smcl
0.0k 9/03/19 10:06 slide3ex1.do
0.0k 9/03/19 10:06 slide3ex2.do
1.1k 9/03/19 10:06 slide4.smcl
0.1k 9/03/19 10:06 slide4ex1.do
0.1k 9/03/19 10:06 slide4ex2.do
0.3k 9/03/19 10:06 slide4ex3.do
1.4k 9/03/19 10:06 slide5.smcl
0.2k 9/03/19 10:06 slide5ex1.do
0.1k 9/03/19 10:06 slide5ex2.do
0.3k 9/03/19 10:06 slide5ex3.do
0.2k 9/03/19 10:06 slide6.smcl
0.8k 9/03/19 10:03 slide7.smcl
0.3k 9/03/19 10:06 stdtable03.smcl
0.3k 9/03/19 9:54 stdtable04.smcl
0.4k 8/08/19 11:46 stdtable05.smcl
0.9k 9/03/19 9:58 stdtable06.smcl
0.9k 8/08/19 11:46 stdtable07.smcl
0.9k 9/03/19 10:03 stdtable08.smcl
. cd ../..
D:\Mijn documenten\projecten\stata\sug\london19\buis_smclpres\presentation
-------------------------------------------------------------------------------
<< index >>
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
How to create a smcl presentation -- creating the presentation
-------------------------------------------------------------------------------
Adding text
You can add a text block by starting a line with /*txt and ending it with
txt*/
The text will be formatted using SMCL, which is documented in help smcl
The most important directives are:
{pstd} starts a standard paragraph
{pmore} starts an indented paragraph
{p_end} ends a paragraph
{help cmd_name} adds a link to the helpfile of cmd_name.
The sourcefile after including text looks like this:
//file homogamy.dta
//section standardizing cross-tabulations
//slide ------------------------------------------------------------------------
//title The influence of marginal distributions
/*txt
{pstd}
Consider the example below
{pstd}
It shows the race of the husband and the race of the wife for couples living in
the USA that got married between 2010 and 2017
{pstd}
The races are very unequaly distributed in the USA
{pstd}
We can control for one marginal distribution by computing row or collumn
percentages.
txt*/
//ex
use homogamy, clear
tab racem racef [fw=freq] if marcoh == 2010, row nofreq
//endex
/*txt
{pstd}
We see racial homogamy: people tend to marry someone of the same race
{pstd}
However, several things are hard to see in this table:
{pmore}
{cmd:Are whites really the most closed group} or is there a substantial
"colorblind" group of whites that accidentally married another white because that
is the largest group?
{pmore}
{cmd:Are Native Americans really so much less homogamous} or are we seeing an
artifact caused by the small number of native american women (0.6%)?
{pmore}
If native Americans were mixing around randomly, then we would expect much less
native american males marrying native american females. Apperently native
American men still prefer native American women but because there are so many
other women around he will still have a good chance of eventually marrying another
women.
{pmore}
{cmd:Is there symetery in this table}, e.g. are hispanic males as likely to marry a
white female as hispanic females are to marry white males?
{pmore}
It does not seem to be the case from this table, but 5% from all white males
could be similar to 18% from all hispanic males.
{pstd}
There is something mechanical about the influence of the margins, and it is
common (in sociology) to want to look at the pattern in the table nett of this
influence of the marginal distributions.
{pstd}
We could do this by looking at odds ratios , but here I want to show an alternative.
txt*/
//endslide ---------------------------------------------------------------------
//slide ------------------------------------------------------------------------
//title Odds ratios
/*txt
{pstd}
The odds is the number of "successes" per "failure"
{pstd}
The odds ratio is a ratio of odds, and this measure of association is indpendent
of the marginal distributions
txt*/
//ex
tab racem racef [fw=freq] if marcoh == 2010
di 122904 / 136200
di 134486 / 31956989
di (122904 / 136200)/(134486 / 31956989)
//endex
/*txt
{pstd}
The odds that a native ameriance man marries a native american women and not a
white women is 0.9.
{pmore}
The odds that a white man marries a native american women and not a white women
is 0.004.
{pstd}
The odds of marrying a native american women compared to a white women is 214
times larger for native American man than for white man.
txt*/
//endslide --------------------------------------------------------------------
//slide ------------------------------------------------------------------------
//title Standardizing tables
/*txt
{pstd}
When we do a chi squared test for cross-tabulations we compare observed cell counts
with predicted cell counts
{pstd}
For these predicted cell counts we assume that the margins remain as observed,
but otherwise there is no association between the variables (the odds ratios are
all 1).
{pstd}
In the table of predicted cell counts the only pattern is due to the margins.
txt*/
//ex
tab racem racef [fw=freq] if marcoh==2010, exp
//endex
/*txt
{pstd}
Can't we reverse that? Keep the association (odds ratios) as observed but fix
the margins.
{pstd}
For example we could fix all margins at a 100.
{pstd}
That way we can look at the proportion native American men marrying native American
women when they weren't such a small group.
{pstd}
This is what standardizing tables does (Yule 1912). This is implemented in the
{helpb stdtable} package.
txt*/
//ex
stdtable racem racef [fw=freq] if marcoh == 2010
//endex
/*txt
{pstd}
{cmd:stdtable} is thus very useful in conjunction with a chi-squared test for
cross-tabulations:
{pmore}
The chi-squared test tells you whether or not there is a pattern in the table
that is significantly different from independence
{pmore}
{cmd:stdtable} tells you what that pattern is.
txt*/
//endslide ---------------------------------------------------------------------
//slide ------------------------------------------------------------------------
//title Displaying results from stdtable
/*txt
{pstd}
We can add options to make the table look better
txt*/
//ex
stdtable racem racef [fw=freq] if marcoh == 2010, ///
format(%5.0f)
//endex
/*txt
We can compare across groups
txt*/
//ex
stdtable racem racef [fw=freq], by(marcoh) format(%5.0f)
//endex
/*txt
{pstd}
Alternatively we can replace the data in memory with standardized counts and
use those to create a graph
txt*/
//ex
qui stdtable racem racef [fw=freq], ///
by(marcoh) replace
tabplot racem marcoh [iw=std], ///
by(racef, compact note("") cols(6) ///
t1title("race, wife")) ///
xlab( 1(1)7, angle(35) labsize(vsmall) )
//endex
//endslide ---------------------------------------------------------------------
//section Estimation
//slide ------------------------------------------------------------------------
//title Iterative Proportional fitting
/*txt
{pstd}
The idea to change the margins to be all 100, but otherwise leave everything as
much as possible the same.
{pstd}
We know how to do that for just row totals:
{pmore}
divide all cells by its rowtotal and multiply by 100
txt*/
//ex
use homogamy, clear
tab racem racef [fw=freq] if marcoh == 2010, matcell(data)
mata
data = st_matrix("data")
muhat = data
muhat = muhat:/rowsum(muhat):*100
end
//endex
/*txt
{pstd}
We could do the same with the column totals
txt*/
//ex
mata
muhat = muhat:/colsum(muhat):*100
colsum(muhat)
rowsum(muhat)
end
//endex
/*txt
{pstd}
This is close, but not quite.
{pstd}
What happens when we repeat that a couple of times
txt*/
//ex
mata
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
colsum(muhat)
rowsum(muhat)
end
//endex
/*txt
{pstd}
Again, better and we can imagine that with some extra iterations we would get
where we want to be.
{pstd}
This is iterative proportional fitting (Kruithof 1937; Deming and Stephan 1940)
txt*/
//endslide ---------------------------------------------------------------------
//slide ------------------------------------------------------------------------
//title Can all tables be standardized?
/*txt
{pstd}Consider the following table{p_end}
0 0 2
1 5 2
8 7 0
{pstd}In order to make the first row total 100, the top right cell {it:must} be
100{p_end}
{pstd}In order to make the last column total 100, the top right cell {it:cannot}
be 100{p_end}
{pstd}This is an example of a table that cannot be standardized, and the algorithm
will not converge.
txt*/
//endslide ---------------------------------------------------------------------
. smclpres using stdtable\source\stdtable04.do , replace dir(stdtable/presentat
> ion)
to view the presentation:
first change the directory to where the presentation is stored:
cd "D:\Mijn
documenten\projecten\stata\sug\london19\buis_smclpres\presentation\stdtable\pre
> sentation"
Then type:
view stdtable04.smcl
-------------------------------------------------------------------------------
<< index >>
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
How to create a smcl presentation -- creating the presentation
-------------------------------------------------------------------------------
Different kinds of slides
The normal slides (what we have used thus far) represent the main linear
flow of the presentation.
We can also add digression slides. The arrows at the bottom of a slide
will skip it, but you must add a link to it in a text block on the
previous regular slide.
So during the presentation, the presenter can easily decide whether or
not to skip the digression slide.
You specify the digression slide using //digr and //enddigr
You specify the where the link will appear in the previous slide
using /*digr*/
You specify the label used for the link using //label
Alternatively we can add a ancillary slide, which can only be accessed
from the index slide
This type of slide serves the purpose of an appendix.
You specify the ancillary slide using //anc and //endanc
The sourcefile after including a digression and an ancillary slide looks
like this:
//file homogamy.dta
//section standardizing cross-tabulations
//slide ------------------------------------------------------------------------
//title The influence of marginal distributions
/*txt
{pstd}
Consider the example below
{pstd}
It shows the race of the husband and the race of the wife for couples living in
the USA that got married between 2010 and 2017
{pstd}
The races are very unequaly distributed in the USA
{pstd}
We can control for one marginal distribution by computing row or collumn
percentages.
txt*/
//ex
use homogamy, clear
tab racem racef [fw=freq] if marcoh == 2010, row nofreq
//endex
/*txt
{pstd}
We see racial homogamy: people tend to marry someone of the same race
{pstd}
However, several things are hard to see in this table:
{pmore}
{cmd:Are whites really the most closed group} or is there a substantial
"colorblind" group of whites that accidentally married another white because that
is the largest group?
{pmore}
{cmd:Are Native Americans really so much less homogamous} or are we seeing an
artifact caused by the small number of native american women (0.6%)?
{pmore}
If native Americans were mixing around randomly, then we would expect much less
native american males marrying native american females. Apperently native
American men still prefer native American women but because there are so many
other women around he will still have a good chance of eventually marrying another
women.
{pmore}
{cmd:Is there symetery in this table}, e.g. are hispanic males as likely to marry a
white female as hispanic females are to marry white males?
{pmore}
It does not seem to be the case from this table, but 5% from all white males
could be similar to 18% from all hispanic males.
{pstd}
There is something mechanical about the influence of the margins, and it is
common (in sociology) to want to look at the pattern in the table nett of this
influence of the marginal distributions.
{pstd}
We could do this by looking at /*digr*/ , but here I want to show an alternative.
txt*/
//endslide ---------------------------------------------------------------------
//digr -------------------------------------------------------------------------
//title Odds ratios
//label odds ratios
/*txt
{pstd}
The odds is the number of "successes" per "failure"
{pstd}
The odds ratio is a ratio of odds, and this measure of association is indpendent
of the marginal distributions
txt*/
//ex
tab racem racef [fw=freq] if marcoh == 2010
di 122904 / 136200
di 134486 / 31956989
di (122904 / 136200)/(134486 / 31956989)
//endex
/*txt
{pstd}
The odds that a native ameriance man marries a native american women and not a
white women is 0.9.
{pmore}
The odds that a white man marries a native american women and not a white women
is 0.004.
{pstd}
The odds of marrying a native american women compared to a white women is 214
times larger for native American man than for white man.
txt*/
//enddigr ----------------------------------------------------------------------
//slide ------------------------------------------------------------------------
//title Standardizing tables
/*txt
{pstd}
When we do a chi squared test for cross-tabulations we compare observed cell counts
with predicted cell counts
{pstd}
For these predicted cell counts we assume that the margins remain as observed,
but otherwise there is no association between the variables (the odds ratios are
all 1).
{pstd}
In the table of predicted cell counts the only pattern is due to the margins.
txt*/
//ex
tab racem racef [fw=freq] if marcoh==2010, exp
//endex
/*txt
{pstd}
Can't we reverse that? Keep the association (odds ratios) as observed but fix
the margins.
{pstd}
For example we could fix all margins at a 100.
{pstd}
That way we can look at the proportion native American men marrying native American
women when they weren't such a small group.
{pstd}
This is what standardizing tables does (Yule 1912). This is implemented in the
{helpb stdtable} package.
txt*/
//ex
stdtable racem racef [fw=freq] if marcoh == 2010
//endex
/*txt
{pstd}
{cmd:stdtable} is thus very useful in conjunction with a chi-squared test for
cross-tabulations:
{pmore}
The chi-squared test tells you whether or not there is a pattern in the table
that is significantly different from independence
{pmore}
{cmd:stdtable} tells you what that pattern is.
txt*/
//endslide ---------------------------------------------------------------------
//slide ------------------------------------------------------------------------
//title Displaying results from stdtable
/*txt
{pstd}
We can add options to make the table look better
txt*/
//ex
stdtable racem racef [fw=freq] if marcoh == 2010, ///
format(%5.0f)
//endex
/*txt
We can compare across groups
txt*/
//ex
stdtable racem racef [fw=freq], by(marcoh) format(%5.0f)
//endex
/*txt
{pstd}
Alternatively we can replace the data in memory with standardized counts and
use those to create a graph
txt*/
//ex
qui stdtable racem racef [fw=freq], ///
by(marcoh) replace
tabplot racem marcoh [iw=std], ///
by(racef, compact note("") cols(6) ///
t1title("race, wife")) ///
xlab( 1(1)7, angle(35) labsize(vsmall) )
//endex
//endslide ---------------------------------------------------------------------
//section Estimation
//slide ------------------------------------------------------------------------
//title Iterative Proportional fitting
/*txt
{pstd}
The idea to change the margins to be all 100, but otherwise leave everything as
much as possible the same.
{pstd}
We know how to do that for just row totals:
{pmore}
divide all cells by its rowtotal and multiply by 100
txt*/
//ex
use homogamy, clear
tab racem racef [fw=freq] if marcoh == 2010, matcell(data)
mata
data = st_matrix("data")
muhat = data
muhat = muhat:/rowsum(muhat):*100
end
//endex
/*txt
{pstd}
We could do the same with the column totals
txt*/
//ex
mata
muhat = muhat:/colsum(muhat):*100
colsum(muhat)
rowsum(muhat)
end
//endex
/*txt
{pstd}
This is close, but not quite.
{pstd}
What happens when we repeat that a couple of times
txt*/
//ex
mata
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
colsum(muhat)
rowsum(muhat)
end
//endex
/*txt
{pstd}
Again, better and we can imagine that with some extra iterations we would get
where we want to be.
{pstd}
This is iterative proportional fitting (Kruithof 1937; Deming and Stephan 1940)
txt*/
//endslide ---------------------------------------------------------------------
//anc --------------------------------------------------------------------------
//title Can all tables be standardized?
/*txt
{pstd}Consider the following table{p_end}
0 0 2
1 5 2
8 7 0
{pstd}In order to make the first row total 100, the top right cell {it:must} be
100{p_end}
{pstd}In order to make the last column total 100, the top right cell {it:cannot}
be 100{p_end}
{pstd}This is an example of a table that cannot be standardized, and the algorithm
will not converge.
txt*/
//endanc -----------------------------------------------------------------------
. smclpres using stdtable\source\stdtable05.do , replace dir(stdtable/presentat
> ion)
to view the presentation:
first change the directory to where the presentation is stored:
cd "D:\Mijn
documenten\projecten\stata\sug\london19\buis_smclpres\presentation\stdtable\pre
> sentation"
Then type:
view stdtable05.smcl
-------------------------------------------------------------------------------
<< index >>
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
How to create a smcl presentation -- creating the presentation
-------------------------------------------------------------------------------
Changing the look of the table of contents
You can specify settings for the overall layout of the presentation using
the //layout command.
For example, //layout toc title(subsection) specifies that the slide
titles are added to the table of content as a subsection.
In our example presentation we add the slide titles to the table of
contents, make those slide titles links rather than the sections, and
make the sections bold
The title of the table of contents can be specified with the //toctitle
command, and you can add text between the title and the table of
contentents with the /*toctxt and toctxt*/ commands
The sourcefile after changing the table contents looks like this:
//layout toc title(subsection) link(subsection) secbold
//file homogamy.dta
//toctitle stdtable, a package to standardize tables
/*toctxt
{center:Maarten L. Buis}
{center:University of Konstanz}
toctxt*/
//section standardizing cross-tabulations
//slide ------------------------------------------------------------------------
//title The influence of marginal distributions
/*txt
{pstd}
Consider the example below
{pstd}
It shows the race of the husband and the race of the wife for couples living in
the USA that got married between 2010 and 2017
{pstd}
The races are very unequaly distributed in the USA
{pstd}
We can control for one marginal distribution by computing row or collumn
percentages.
txt*/
//ex
use homogamy, clear
tab racem racef [fw=freq] if marcoh == 2010, row nofreq
//endex
/*txt
{pstd}
We see racial homogamy: people tend to marry someone of the same race
{pstd}
However, several things are hard to see in this table:
{pmore}
{cmd:Are whites really the most closed group} or is there a substantial
"colorblind" group of whites that accidentally married another white because that
is the largest group?
{pmore}
{cmd:Are Native Americans really so much less homogamous} or are we seeing an
artifact caused by the small number of native american women (0.6%)?
{pmore}
If native Americans were mixing around randomly, then we would expect much less
native american males marrying native american females. Apperently native
American men still prefer native American women but because there are so many
other women around he will still have a good chance of eventually marrying another
women.
{pmore}
{cmd:Is there symetery in this table}, e.g. are hispanic males as likely to marry a
white female as hispanic females are to marry white males?
{pmore}
It does not seem to be the case from this table, but 5% from all white males
could be similar to 18% from all hispanic males.
{pstd}
There is something mechanical about the influence of the margins, and it is
common (in sociology) to want to look at the pattern in the table nett of this
influence of the marginal distributions.
{pstd}
We could do this by looking at /*digr*/ , but here I want to show an alternative.
txt*/
//endslide ---------------------------------------------------------------------
//digr -------------------------------------------------------------------------
//title Odds ratios
//label odds ratios
/*txt
{pstd}
The odds is the number of "successes" per "failure"
{pstd}
The odds ratio is a ratio of odds, and this measure of association is indpendent
of the marginal distributions
txt*/
//ex
tab racem racef [fw=freq] if marcoh == 2010
di 122904 / 136200
di 134486 / 31956989
di (122904 / 136200)/(134486 / 31956989)
//endex
/*txt
{pstd}
The odds that a native ameriance man marries a native american women and not a
white women is 0.9.
{pmore}
The odds that a white man marries a native american women and not a white women
is 0.004.
{pstd}
The odds of marrying a native american women compared to a white women is 214
times larger for native American man than for white man.
txt*/
//enddigr ----------------------------------------------------------------------
//slide ------------------------------------------------------------------------
//title Standardizing tables
/*txt
{pstd}
When we do a chi squared test for cross-tabulations we compare observed cell counts
with predicted cell counts
{pstd}
For these predicted cell counts we assume that the margins remain as observed,
but otherwise there is no association between the variables (the odds ratios are
all 1).
{pstd}
In the table of predicted cell counts the only pattern is due to the margins.
txt*/
//ex
tab racem racef [fw=freq] if marcoh==2010, exp
//endex
/*txt
{pstd}
Can't we reverse that? Keep the association (odds ratios) as observed but fix
the margins.
{pstd}
For example we could fix all margins at a 100.
{pstd}
That way we can look at the proportion native American men marrying native American
women when they weren't such a small group.
{pstd}
This is what standardizing tables does (Yule 1912). This is implemented in the
{helpb stdtable} package.
txt*/
//ex
stdtable racem racef [fw=freq] if marcoh == 2010
//endex
/*txt
{pstd}
{cmd:stdtable} is thus very useful in conjunction with a chi-squared test for
cross-tabulations:
{pmore}
The chi-squared test tells you whether or not there is a pattern in the table
that is significantly different from independence
{pmore}
{cmd:stdtable} tells you what that pattern is.
txt*/
//endslide ---------------------------------------------------------------------
//slide ------------------------------------------------------------------------
//title Displaying results from stdtable
/*txt
{pstd}
We can add options to make the table look better
txt*/
//ex
stdtable racem racef [fw=freq] if marcoh == 2010, ///
format(%5.0f)
//endex
/*txt
We can compare across groups
txt*/
//ex
stdtable racem racef [fw=freq], by(marcoh) format(%5.0f)
//endex
/*txt
{pstd}
Alternatively we can replace the data in memory with standardized counts and
use those to create a graph
txt*/
//ex
qui stdtable racem racef [fw=freq], ///
by(marcoh) replace
tabplot racem marcoh [iw=std], ///
by(racef, compact note("") cols(6) ///
t1title("race, wife")) ///
xlab( 1(1)7, angle(35) labsize(vsmall) )
//endex
//endslide ---------------------------------------------------------------------
//section Estimation
//slide ------------------------------------------------------------------------
//title Iterative Proportional fitting
/*txt
{pstd}
The idea to change the margins to be all 100, but otherwise leave everything as
much as possible the same.
{pstd}
We know how to do that for just row totals:
{pmore}
divide all cells by its rowtotal and multiply by 100
txt*/
//ex
use homogamy, clear
tab racem racef [fw=freq] if marcoh == 2010, matcell(data)
mata
data = st_matrix("data")
muhat = data
muhat = muhat:/rowsum(muhat):*100
end
//endex
/*txt
{pstd}
We could do the same with the column totals
txt*/
//ex
mata
muhat = muhat:/colsum(muhat):*100
colsum(muhat)
rowsum(muhat)
end
//endex
/*txt
{pstd}
This is close, but not quite.
{pstd}
What happens when we repeat that a couple of times
txt*/
//ex
mata
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
colsum(muhat)
rowsum(muhat)
end
//endex
/*txt
{pstd}
Again, better and we can imagine that with some extra iterations we would get
where we want to be.
{pstd}
This is iterative proportional fitting (Kruithof 1937; Deming and Stephan 1940)
txt*/
//endslide ---------------------------------------------------------------------
//anc --------------------------------------------------------------------------
//title Can all tables be standardized?
/*txt
{pstd}Consider the following table{p_end}
0 0 2
1 5 2
8 7 0
{pstd}In order to make the first row total 100, the top right cell {it:must} be
100{p_end}
{pstd}In order to make the last column total 100, the top right cell {it:cannot}
be 100{p_end}
{pstd}This is an example of a table that cannot be standardized, and the algorithm
will not converge.
txt*/
//endanc -----------------------------------------------------------------------
. smclpres using stdtable\source\stdtable06.do , replace dir(stdtable/presentat
> ion)
to view the presentation:
first change the directory to where the presentation is stored:
cd "D:\Mijn
documenten\projecten\stata\sug\london19\buis_smclpres\presentation\stdtable\pre
> sentation"
Then type:
view stdtable06.smcl
-------------------------------------------------------------------------------
<< index >>
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
How to create a smcl presentation -- creating the presentation
-------------------------------------------------------------------------------
Adding references
You can add references from a BibTex library to a smclpres presentation.
You tell smclpres which library to use with //layout bib
bibfile(bibtex_file)
After that you add references using /*cite bibtex_key */
At the end of the presentation you add the references-slide using //bib
and //endbib, and within that slide indicate where the references are to
appear with //bib_here.
The sourcefile after adding references looks like this:
//layout toc title(subsection) link(subsection) secbold
//layout bib bibfile(standardize.bib)
//file homogamy.dta
//toctitle stdtable, a package to standardize tables
/*toctxt
{center:Maarten L. Buis}
{center:University of Konstanz}
toctxt*/
//section standardizing cross-tabulations
//slide ------------------------------------------------------------------------
//title The influence of marginal distributions
/*txt
{pstd}
Consider the example below
{pstd}
It shows the race of the husband and the race of the wife for couples living in
the USA that got married between 2010 and 2017
{pstd}
The races are very unequaly distributed in the USA
{pstd}
We can control for one marginal distribution by computing row or collumn
percentages.
txt*/
//ex
use homogamy, clear
tab racem racef [fw=freq] if marcoh == 2010, row nofreq
//endex
/*txt
{pstd}
We see racial homogamy: people tend to marry someone of the same race
{pstd}
However, several things are hard to see in this table:
{pmore}
{cmd:Are whites really the most closed group} or is there a substantial
"colorblind" group of whites that accidentally married another white because that
is the largest group?
{pmore}
{cmd:Are Native Americans really so much less homogamous} or are we seeing an
artifact caused by the small number of native american women (0.6%)?
{pmore}
If native Americans were mixing around randomly, then we would expect much less
native american males marrying native american females. Apperently native
American men still prefer native American women but because there are so many
other women around he will still have a good chance of eventually marrying another
women.
{pmore}
{cmd:Is there symetery in this table}, e.g. are hispanic males as likely to marry a
white female as hispanic females are to marry white males?
{pmore}
It does not seem to be the case from this table, but 5% from all white males
could be similar to 18% from all hispanic males.
{pstd}
There is something mechanical about the influence of the margins, and it is
common (in sociology) to want to look at the pattern in the table nett of this
influence of the marginal distributions.
{pstd}
We could do this by looking at /*digr*/ , but here I want to show an alternative.
txt*/
//endslide ---------------------------------------------------------------------
//digr -------------------------------------------------------------------------
//title Odds ratios
//label odds ratios
/*txt
{pstd}
The odds is the number of "successes" per "failure"
{pstd}
The odds ratio is a ratio of odds, and this measure of association is indpendent
of the marginal distributions
txt*/
//ex
tab racem racef [fw=freq] if marcoh == 2010
di 122904 / 136200
di 134486 / 31956989
di (122904 / 136200)/(134486 / 31956989)
//endex
/*txt
{pstd}
The odds that a native ameriance man marries a native american women and not a
white women is 0.9.
{pmore}
The odds that a white man marries a native american women and not a white women
is 0.004.
{pstd}
The odds of marrying a native american women compared to a white women is 214
times larger for native American man than for white man.
txt*/
//enddigr ----------------------------------------------------------------------
//slide ------------------------------------------------------------------------
//title Standardizing tables
/*txt
{pstd}
When we do a chi squared test for cross-tabulations we compare observed cell counts
with predicted cell counts
{pstd}
For these predicted cell counts we assume that the margins remain as observed,
but otherwise there is no association between the variables (the odds ratios are
all 1).
{pstd}
In the table of predicted cell counts the only pattern is due to the margins.
txt*/
//ex
tab racem racef [fw=freq] if marcoh==2010, exp
//endex
/*txt
{pstd}
Can't we reverse that? Keep the association (odds ratios) as observed but fix
the margins.
{pstd}
For example we could fix all margins at a 100.
{pstd}
That way we can look at the proportion native American men marrying native American
women when they weren't such a small group.
{pstd}
This is what standardizing tables does /*cite yule12 */. This is implemented in the
{helpb stdtable} package.
txt*/
//ex
stdtable racem racef [fw=freq] if marcoh == 2010
//endex
/*txt
{pstd}
{cmd:stdtable} is thus very useful in conjunction with a chi-squared test for
cross-tabulations:
{pmore}
The chi-squared test tells you whether or not there is a pattern in the table
that is significantly different from independence
{pmore}
{cmd:stdtable} tells you what that pattern is.
txt*/
//endslide ---------------------------------------------------------------------
//slide ------------------------------------------------------------------------
//title Displaying results from stdtable
/*txt
{pstd}
We can add options to make the table look better
txt*/
//ex
stdtable racem racef [fw=freq] if marcoh == 2010, ///
format(%5.0f)
//endex
/*txt
We can compare across groups
txt*/
//ex
stdtable racem racef [fw=freq], by(marcoh) format(%5.0f)
//endex
/*txt
{pstd}
Alternatively we can replace the data in memory with standardized counts and
use those to create a graph
txt*/
//ex
qui stdtable racem racef [fw=freq], ///
by(marcoh) replace
tabplot racem marcoh [iw=std], ///
by(racef, compact note("") cols(6) ///
t1title("race, wife")) ///
xlab( 1(1)7, angle(35) labsize(vsmall) )
//endex
//endslide ---------------------------------------------------------------------
//section Estimation
//slide ------------------------------------------------------------------------
//title Iterative Proportional fitting
/*txt
{pstd}
The idea to change the margins to be all 100, but otherwise leave everything as
much as possible the same.
{pstd}
We know how to do that for just row totals:
{pmore}
divide all cells by its rowtotal and multiply by 100
txt*/
//ex
use homogamy, clear
tab racem racef [fw=freq] if marcoh == 2010, matcell(data)
mata
data = st_matrix("data")
muhat = data
muhat = muhat:/rowsum(muhat):*100
end
//endex
/*txt
{pstd}
We could do the same with the column totals
txt*/
//ex
mata
muhat = muhat:/colsum(muhat):*100
colsum(muhat)
rowsum(muhat)
end
//endex
/*txt
{pstd}
This is close, but not quite.
{pstd}
What happens when we repeat that a couple of times
txt*/
//ex
mata
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
colsum(muhat)
rowsum(muhat)
end
//endex
/*txt
{pstd}
Again, better and we can imagine that with some extra iterations we would get
where we want to be.
{pstd}
This is iterative proportional fitting /*cite kruithof37 deming_stephan40 */
txt*/
//endslide ---------------------------------------------------------------------
//anc --------------------------------------------------------------------------
//title Can all tables be standardized?
/*txt
{pstd}Consider the following table{p_end}
0 0 2
1 5 2
8 7 0
{pstd}In order to make the first row total 100, the top right cell {it:must} be
100{p_end}
{pstd}In order to make the last column total 100, the top right cell {it:cannot}
be 100{p_end}
{pstd}This is an example of a table that cannot be standardized, and the algorithm
will not converge.
txt*/
//endanc -----------------------------------------------------------------------
//bib --------------------------------------------------------------------------
//title References
//bib_here
//endbib -----------------------------------------------------------------------
. smclpres using stdtable\source\stdtable07.do , replace dir(stdtable/presentat
> ion)
to view the presentation:
first change the directory to where the presentation is stored:
cd "D:\Mijn
documenten\projecten\stata\sug\london19\buis_smclpres\presentation\stdtable\pre
> sentation"
Then type:
view stdtable07.smcl
-------------------------------------------------------------------------------
<< index >>
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
How to create a smcl presentation -- creating a handout
-------------------------------------------------------------------------------
Initial handout
.smcl presentations are good at illustrating how to use Stata
However, they are inconvenient for the audience if they later want to
look something up from that presentation
The pres2html command will turn a .smcl presentation into a .html handout
cd stdtable/presentation
pres2html using stdtable07.smcl, dir(../handout) replace
cd ../..
-------------------------------------------------------------------------------
<< index >>
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
How to create a smcl presentation -- creating a handout
-------------------------------------------------------------------------------
Adding graphs to the handout
Notice that the graph is not displayed in the handout
You can tell pres2html that a graph needs to be added with the command
//graph graphname.
The sourcefile after adding that looks like this:
//layout toc title(subsection) link(subsection) secbold
//layout bib bibfile(standardize.bib)
//file homogamy.dta
//toctitle stdtable, a package to standardize tables
/*toctxt
{center:Maarten L. Buis}
{center:University of Konstanz}
toctxt*/
//section standardizing cross-tabulations
//slide ------------------------------------------------------------------------
//title The influence of marginal distributions
/*txt
{pstd}
Consider the example below
{pstd}
It shows the race of the husband and the race of the wife for couples living in
the USA that got married between 2010 and 2017
{pstd}
The races are very unequaly distributed in the USA
{pstd}
We can control for one marginal distribution by computing row or collumn
percentages.
txt*/
//ex
use homogamy, clear
tab racem racef [fw=freq] if marcoh == 2010, row nofreq
//endex
/*txt
{pstd}
We see racial homogamy: people tend to marry someone of the same race
{pstd}
However, several things are hard to see in this table:
{pmore}
{cmd:Are whites really the most closed group} or is there a substantial
"colorblind" group of whites that accidentally married another white because that
is the largest group?
{pmore}
{cmd:Are Native Americans really so much less homogamous} or are we seeing an
artifact caused by the small number of native american women (0.6%)?
{pmore}
If native Americans were mixing around randomly, then we would expect much less
native american males marrying native american females. Apperently native
American men still prefer native American women but because there are so many
other women around he will still have a good chance of eventually marrying another
women.
{pmore}
{cmd:Is there symetery in this table}, e.g. are hispanic males as likely to marry a
white female as hispanic females are to marry white males?
{pmore}
It does not seem to be the case from this table, but 5% from all white males
could be similar to 18% from all hispanic males.
{pstd}
There is something mechanical about the influence of the margins, and it is
common (in sociology) to want to look at the pattern in the table nett of this
influence of the marginal distributions.
{pstd}
We could do this by looking at /*digr*/ , but here I want to show an alternative.
txt*/
//endslide ---------------------------------------------------------------------
//digr -------------------------------------------------------------------------
//title Odds ratios
//label odds ratios
/*txt
{pstd}
The odds is the number of "successes" per "failure"
{pstd}
The odds ratio is a ratio of odds, and this measure of association is indpendent
of the marginal distributions
txt*/
//ex
tab racem racef [fw=freq] if marcoh == 2010
di 122904 / 136200
di 134486 / 31956989
di (122904 / 136200)/(134486 / 31956989)
//endex
/*txt
{pstd}
The odds that a native ameriance man marries a native american women and not a
white women is 0.9.
{pmore}
The odds that a white man marries a native american women and not a white women
is 0.004.
{pstd}
The odds of marrying a native american women compared to a white women is 214
times larger for native American man than for white man.
txt*/
//enddigr ---------------------------------------------------------------------
//slide ------------------------------------------------------------------------
//title Standardizing tables
/*txt
{pstd}
When we do a chi squared test for cross-tabulations we compare observed cell counts
with predicted cell counts
{pstd}
For these predicted cell counts we assume that the margins remain as observed,
but otherwise there is no association between the variables (the odds ratios are
all 1).
{pstd}
In the table of predicted cell counts the only pattern is due to the margins.
txt*/
//ex
tab racem racef [fw=freq] if marcoh==2010, exp
//endex
/*txt
{pstd}
Can't we reverse that? Keep the association (odds ratios) as observed but fix
the margins.
{pstd}
For example we could fix all margins at a 100.
{pstd}
That way we can look at the proportion native American men marrying native American
women when they weren't such a small group.
{pstd}
This is what standardizing tables does /*cite yule12 */. This is implemented in the
{helpb stdtable} package.
txt*/
//ex
stdtable racem racef [fw=freq] if marcoh == 2010
//endex
/*txt
{pstd}
{cmd:stdtable} is thus very useful in conjunction with a chi-squared test for
cross-tabulations:
{pmore}
The chi-squared test tells you whether or not there is a pattern in the table
that is significantly different from independence
{pmore}
{cmd:stdtable} tells you what that pattern is.
txt*/
//endslide ---------------------------------------------------------------------
//slide ------------------------------------------------------------------------
//title Displaying results from stdtable
/*txt
{pstd}
We can add options to make the table look better
txt*/
//ex
stdtable racem racef [fw=freq] if marcoh == 2010, ///
format(%5.0f)
//endex
/*txt
We can compare across groups
txt*/
//ex
stdtable racem racef [fw=freq], by(marcoh) format(%5.0f)
//endex
/*txt
{pstd}
Alternatively we can replace the data in memory with standardized counts and
use those to create a graph
txt*/
//ex
qui stdtable racem racef [fw=freq], ///
by(marcoh) replace
tabplot racem marcoh [iw=std], ///
by(racef, compact note("") cols(6) ///
t1title("race, wife")) ///
xlab( 1(1)7, angle(35) labsize(vsmall) )
//endex
//graph Graph
//endslide ---------------------------------------------------------------------
//section Estimation
//slide ------------------------------------------------------------------------
//title Iterative Proportional fitting
/*txt
{pstd}
The idea to change the margins to be all 100, but otherwise leave everything as
much as possible the same.
{pstd}
We know how to do that for just row totals:
{pmore}
divide all cells by its rowtotal and multiply by 100
txt*/
//ex
use homogamy, clear
tab racem racef [fw=freq] if marcoh == 2010, matcell(data)
mata
data = st_matrix("data")
muhat = data
muhat = muhat:/rowsum(muhat):*100
end
//endex
/*txt
{pstd}
We could do the same with the column totals
txt*/
//ex
mata
muhat = muhat:/colsum(muhat):*100
colsum(muhat)
rowsum(muhat)
end
//endex
/*txt
{pstd}
This is close, but not quite.
{pstd}
What happens when we repeat that a couple of times
txt*/
//ex
mata
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
muhat = muhat:/rowsum(muhat):*100
muhat = muhat:/colsum(muhat):*100
colsum(muhat)
rowsum(muhat)
end
//endex
/*txt
{pstd}
Again, better and we can imagine that with some extra iterations we would get
where we want to be.
{pstd}
This is iterative proportional fitting /*cite kruithof37 deming_stephan40 */
txt*/
//endslide ---------------------------------------------------------------------
//anc --------------------------------------------------------------------------
//title Can all tables be standardized?
/*txt
{pstd}Consider the following table{p_end}
0 0 2
1 5 2
8 7 0
{pstd}In order to make the first row total 100, the top right cell {it:must} be
100{p_end}
{pstd}In order to make the last column total 100, the top right cell {it:cannot}
be 100{p_end}
{pstd}This is an example of a table that cannot be standardized, and the algorithm
will not converge.
txt*/
//endanc -----------------------------------------------------------------------
//bib --------------------------------------------------------------------------
//title References
//bib_here
//endbib -----------------------------------------------------------------------
smclpres using stdtable/source/stdtable08.do , replace
dir(stdtable/presentation)
pres2html using stdtable/presentation/stdtable08.smcl, replace
dir(stdtable/handout)
-------------------------------------------------------------------------------
<< index >>
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
How to create a smcl presentation -- creating a handout
-------------------------------------------------------------------------------
Adding contents or output of a .do file to the handout
In this presentation I added a lot of links to .do files. In the handout
we would want a copy of those .do files in the handout.
This can be done using the //codefile filename label command.
In a teaching context I use this when including some small excercises
with the solution in the .do file.
-------------------------------------------------------------------------------
<< index
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
digression
-------------------------------------------------------------------------------
Odds ratios
The odds is the number of "successes" per "failure"
The odds ratio is a ratio of odds, and this measure of association is
indpendent of the marginal distributions
. tab racem racef [fw=freq] if marcoh == 2010
race, | race, wife
husband | white hispanic black native asian | Total
-----------+-------------------------------------------------------+----------
white |31,956,989 1,842,451 270,679 134,486 911,938 |35,687,890
hispanic | 1,716,537 7,292,537 111,903 25,163 145,556 | 9,404,856
black | 674,410 282,817 4,014,816 12,534 72,745 | 5,181,272
native | 136,200 20,397 4,253 122,904 6,469 | 295,799
asian | 323,750 85,783 13,922 2,216 2,820,542 | 3,293,314
other | 494,673 123,760 55,546 7,248 83,703 | 1,068,672
-----------+-------------------------------------------------------+----------
Total |35,302,559 9,647,745 4,471,119 304,551 4,040,953 |54,931,803
race, | race, wife
husband | other | Total
-----------+-----------+----------
white | 571,347 |35,687,890
hispanic | 113,160 | 9,404,856
black | 123,950 | 5,181,272
native | 5,576 | 295,799
asian | 47,101 | 3,293,314
other | 303,742 | 1,068,672
-----------+-----------+----------
Total | 1,164,876 |54,931,803
. di 122904 / 136200
.90237885
. di 134486 / 31956989
.00420834
. di (122904 / 136200)/(134486 / 31956989)
214.42612
The odds that a native ameriance man marries a native american women and
not a white women is 0.9.
The odds that a white man marries a native american women and not a
white women is 0.004.
The odds of marrying a native american women compared to a white women is
214 times larger for native American man than for white man.
-------------------------------------------------------------------------------
<< index
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
ancillary
-------------------------------------------------------------------------------
Can all tables be standardized?
Consider the following table
0 0 2
1 5 2
8 7 0
In order to make the first row total 100, the top right cell must be 100
In order to make the last column total 100, the top right cell cannot be
100
This is an example of a table that cannot be standardized, and the
algorithm will not converge.
-------------------------------------------------------------------------------
index
-------------------------------------------------------------------------------
References
Deming, W. Edwards and Stephan, Frederick F. (1940), "On a Least Squares
Adjustment of a Sampled Frequency Table When the Expected Marginal
Totals are Known", The Annals of Mathematical Statistics, 11(4), pp.
427--444.
Kruithof, J. (1937), "Telefoonverkeersrekening", De Ingenieur, 52(8), pp.
E15-E25.
Yule, G. Udny (1912), "On the Methods of Measuring Association Between
Two Attributes", Journal of the Royal Statistical Society, 75(6), pp.
579-652.
-------------------------------------------------------------------------------
index
-------------------------------------------------------------------------------
