Maarten L. Buis

• Overview
• Curriculum Vitae
• Publications
• Dissertation
• Working papers
• Presentations
• Workshops
• ⇒ Software
• Stata example FAQ
• Links

asl_norm

Author: Maarten L. Buis

asl_norm computes bootstrap estimates of the Achieved Significance Levels (ASL) for a number of Gaussianity (normality) tests. This ASL can be interpreted as a more robust estimate of the p-value and/or as a simulation check of whether the chosen statistic is working well in your sample, i.e. whether the ASL corresponds with the asymptotic p-value.

This package can be installed by typing in Stata: ssc install asl_norm

Example

In a small sample most tests have at least some degree of trouble. In this case (74 observations) the Doornik-Hansen test leads to a p-value that is a bit too large.

. sysuse auto, clear
(1978 Automobile Data)

. asl_norm trunk, dh reps(19999) nodots


Doornik-Hansen test statistic (chi2(2)):    1.91  
asymptotic p-value:                         0.3840
achieved significance level (ASL):          0.3577
95% Monte Carlo CI for ASL:                 [0.3511, 0.3643]

[do-file]

In larger samples the asymptotic p-values tend to be less problematic

. sysuse nlsw88, clear
(NLSW, 1988 extract)

. gen lnwage = ln(wage)

. asl_norm lnwage if union < ., dh reps(19999) nodots


Doornik-Hansen test statistic (chi2(2)):    2.80  
asymptotic p-value:                         0.2465
achieved significance level (ASL):          0.2459
95% Monte Carlo CI for ASL:                 [0.2399, 0.2518]

[do-file]

You can use the saving() option to perform a simulation of how well the tests perform for the number of observations in your dataset. This creates a dataset of test statistics on datasets where the null hypothesis is true, so the distribution of these statistics should correspond to the theoretical sampling distribution and the p-values should follow a continuous standard uniform distribution. This example requires the qenv, qplot, and simpplot packages.

. set seed 12345

. sysuse auto, clear
(1978 Automobile Data)

. 
. tempfile res

. asl_norm trunk, jb sktest reps(19999) saving("`res'") nodots


Skewness/Kurtosis test statistic (chi2(2)): 4.19  
asymptotic p-value:                         0.1228
achieved significance level (ASL):          0.1298
95% Monte Carlo CI for ASL:                 [0.1252, 0.1345]


Jarque-Bera test statistic (chi2(2)):       2.02  
asymptotic p-value:                         0.3636
achieved significance level (ASL):          0.2548
95% Monte Carlo CI for ASL:                 [0.2488, 0.2608]

. use "`res'"

. 
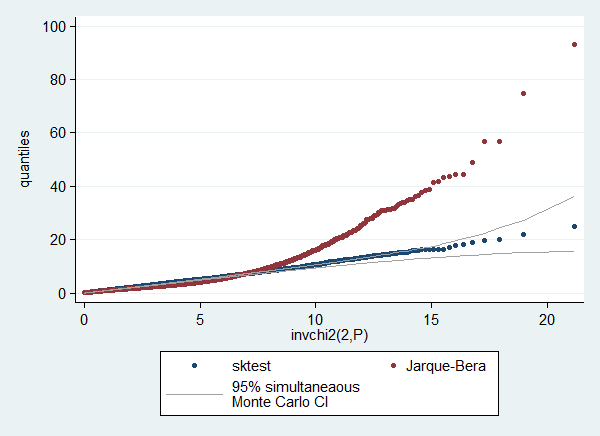
. // check sampling distribution of test statistic
. qenvchi2 sktest, gen(lb ub) df(2) overall reps(19999)

. qplot sktest jbtest lb ub, trscale(invchi2(2,@)) ///
>       ms(o o none ..) c(. . l l)  lc(gs10 ..)    ///
>       scheme(s2color) ylab(,angle(horizontal))   ///
>       legend(order( 1 "sktest"                   ///
>                     2 "Jarque-Bera"              ///
>                     3 "95% simultaneaous"        ///
>                       "Monte Carlo CI"))         

. 
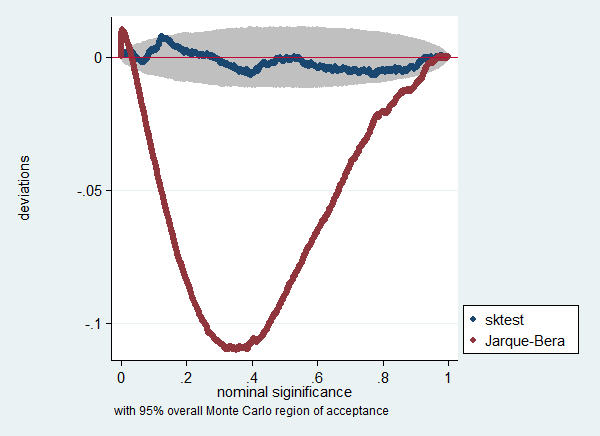
. // test sampling distribution of p-values
. gen p_sk = chi2tail(2,sktest)

. label var p_sk "sktest"

. gen p_jb = chi2tail(2,jbtest)

. label var p_jb "Jarque-Bera"

. simpplot p_sk p_jb, overall reps(19999)          ///
>          scheme(s2color) ylab(,angle(horizontal))

[do-file]